Lab 10: Path Planning and Execution
Objective
The purpose of this lab is to implement path planning to enable the robot to move from an unknown position to a goal position.
Simulator
Map to Grid
To perform path planning, I separated the map into grids so I can store a 1 or a 0 in a grid position depending on if there is a wall there or not. In the simulator, I updated the map with the actual map I will be using with the real robot. I did this by running the code provided and pasting the result into the playground.world document in the world folder. I had to be careful with grid orientation vs world orientation, I had to flip the y axis and move the (0,0) position on the xy axis to (0,0) position in the grid frame which is when: row = 1, column = 1. As shown below, the actual map broken down into grid format: After performing this task, I was able to acquire a 2D matrix with 1s and 0s, as shown below, that can be used to perform localization, and path planning. The 1s are where the wall is present, and 0s are where there is an open space. I used MATLAB to plot the matrix representation of the walls on the grid to show the accuracy of the grid format, as shown below. Initially, the matrix format was flipped and ended up missing half the walls on the map. After debugging, I discovered that I was confusing the number of cells with the number of lines that create these cells, therefore, causing me to exclude the cells on the edges. As shown below, you can see the comparison between the actual map and the grid map. The figure includes the following:- Red line - Actual map
- Green dots - Grid representation of the map from the matrix
- Blue cross - Random Start point
- Red cross - Pre-determined goal point
Matlab Code
% ECE 4960 - Lab 10
% Convert xy coordinates of map to grid coordinates
close all; clear; clc;
points = [0, 0;
0, 0.8;
0.21, 1.1684;
1.0414,1.1684;
1.0414,0;
0,0;
0.4826,0.6604;
0.6858,0.6604;
0.6858,0.508;
0.4826,0.508;
0.4826,0.6604];
maxX = max(points(:,1));
maxY = max(points(:,2));
n = 20;
dx = maxX/(n-1);
dy = maxY/(n-1);
xgrid = 0:dx:maxX;
ygrid = flip(0:dy:maxY);
xplot = ones(n+1,n+1).*(-dx/2:dx:maxX+dx/2);
yplot = flip(ones(n+1,n+1).*(-dy/2:dy:maxY+dy/2)',1);
figure(1)
axis off
hold on
plot(points(1:6,1),points(1:6,2),'r','linewidth',2)
plot(points(7:11,1),points(7:11,2),'r','linewidth',2)
plot(xplot,yplot,'k')
plot(xplot',yplot','k')
hold off
% break down points into multiple points
P = [];
for i = 1:5 % border
xp = points(i,1); %prev
yp = points(i,2);
xn = points(i+1,1); %next
yn = points(i+1,2);
px = linspace(xp,xn)';
py = linspace(yp,yn)';
P = [P;[px,py]];
end
for i = 7:10 % border
xp = points(i,1); %prev
yp = points(i,2);
xn = points(i+1,1); %next
yn = points(i+1,2);
px = linspace(xp,xn)';
py = linspace(yp,yn)';
P = [P;[px,py]];
end
% Get an array for the grid
x = (-dx/2:dx:maxX+dx/2);
y = flip(-dy/2:dy:maxY+dy/2);
grid = zeros(n,n);
for p = 1:size(P,1)
% If map in cell
% if p == 800
% ha = input('stop');
% end
px = P(p,1); py = P(p,2);
C = find(px<=x); c = C(1)-1;
R = find(py<=y); r = R(end);
grid(r,c) = 1;
end
xgrid_plot = []; ygrid_plot = [];
for r = 1:n
for c = 1:n
if grid(r,c) == 1
xgrid_plot = [xgrid_plot;xgrid(c)];
ygrid_plot = [ygrid_plot;ygrid(r)];
end
end
end
figure(1); hold on;
plot(xgrid_plot,ygrid_plot,'go','linewidth',3)
Path planning
I transferred this 2D matrix into jupyter and plotted it, as shown below. The result is as expected, and this means I can move forward with this grid representation to simulate the path planning algorithm. I duplicated the code from Lab 9 and the only part I changed is the trajectory function because this function determines the velocity inputs to the robot. This was useful to me because the algorithm I chose gave me waypoints that I can step on to get to the goal point, and I can use these waypoints to determine the deflection needed for the robot at each time step. I chose an arbitrary value for time (dt = 1 second) and converted these deflections into velocity inputs for the robot.Algorithm
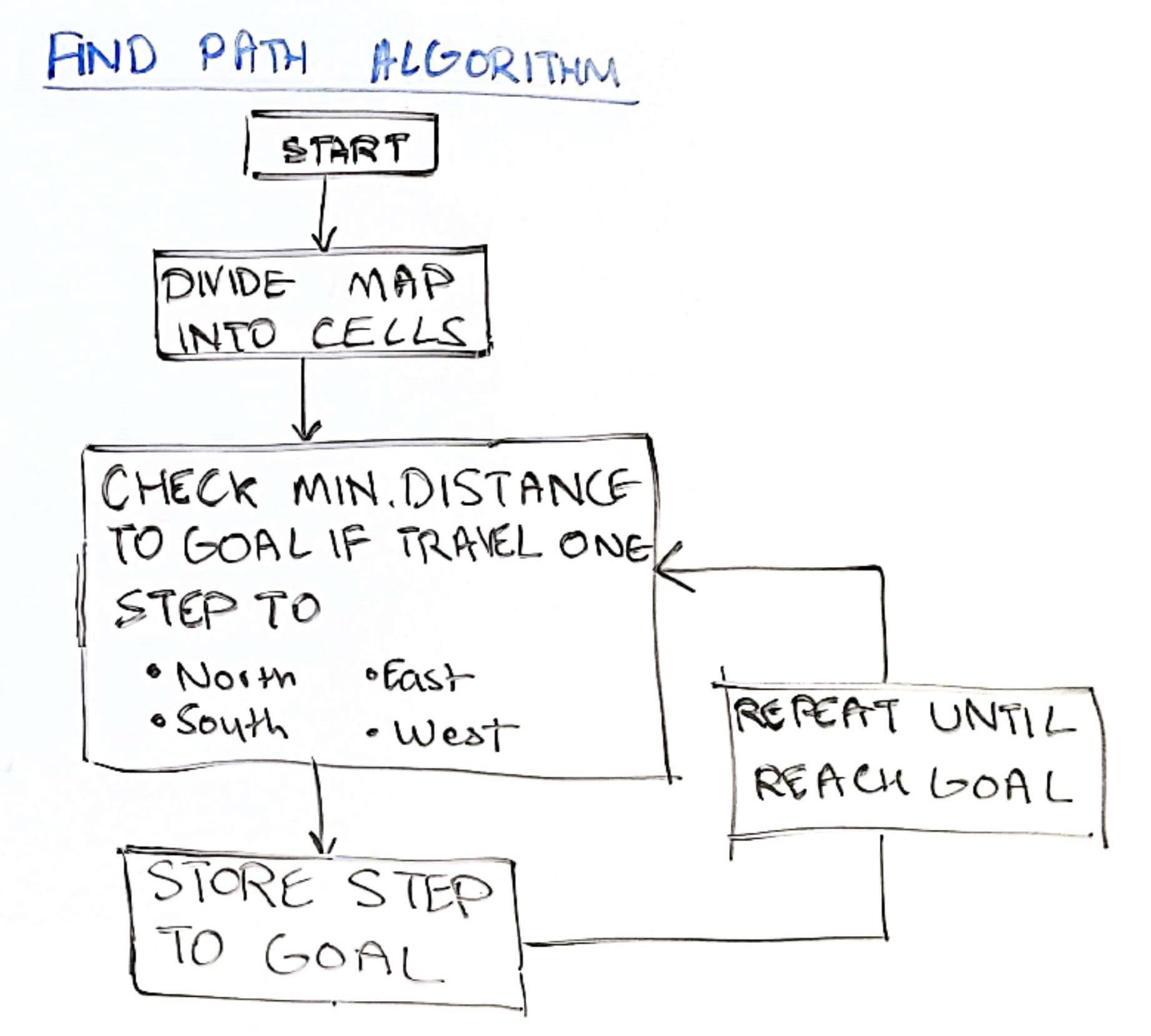
In order to perform the tasks mentioned above, I needed a method to get these waypoints that were leading the robot from an unknown start position to a known goal position. This process is summarized in the image shown below, however, to understand the process better, I will explain it in steps: At each time step, the robot will do the following:- Convert map from global coordinates to grid coordinates
-
Given: The start position and the goal position prior to this algorithm.
Determine the minimum distance from the goal grid position to the new position after the robot moves either North, South, East, or West, from the previous cell. Depending on which direction provides the minimum distance, the robot's future step is stored in a matrix.
Important: At each step, if there is a wall in either of the directions, that direction is disregarded. - Repeat this process, until the goal position has been reached.
-
Once the algorithm has finished and the goal point is reached, I used this matrix of directions
to determine the velocity inputs sent to the robot. For example, assume that the robot starts
at 0 degrees (i.e. facing east) then if the direction was:
- North: Rotate +90 degrees
- South: Rotate -90 degrees
- East: Rotate +0 degrees
- West: Rotate +180 degrees
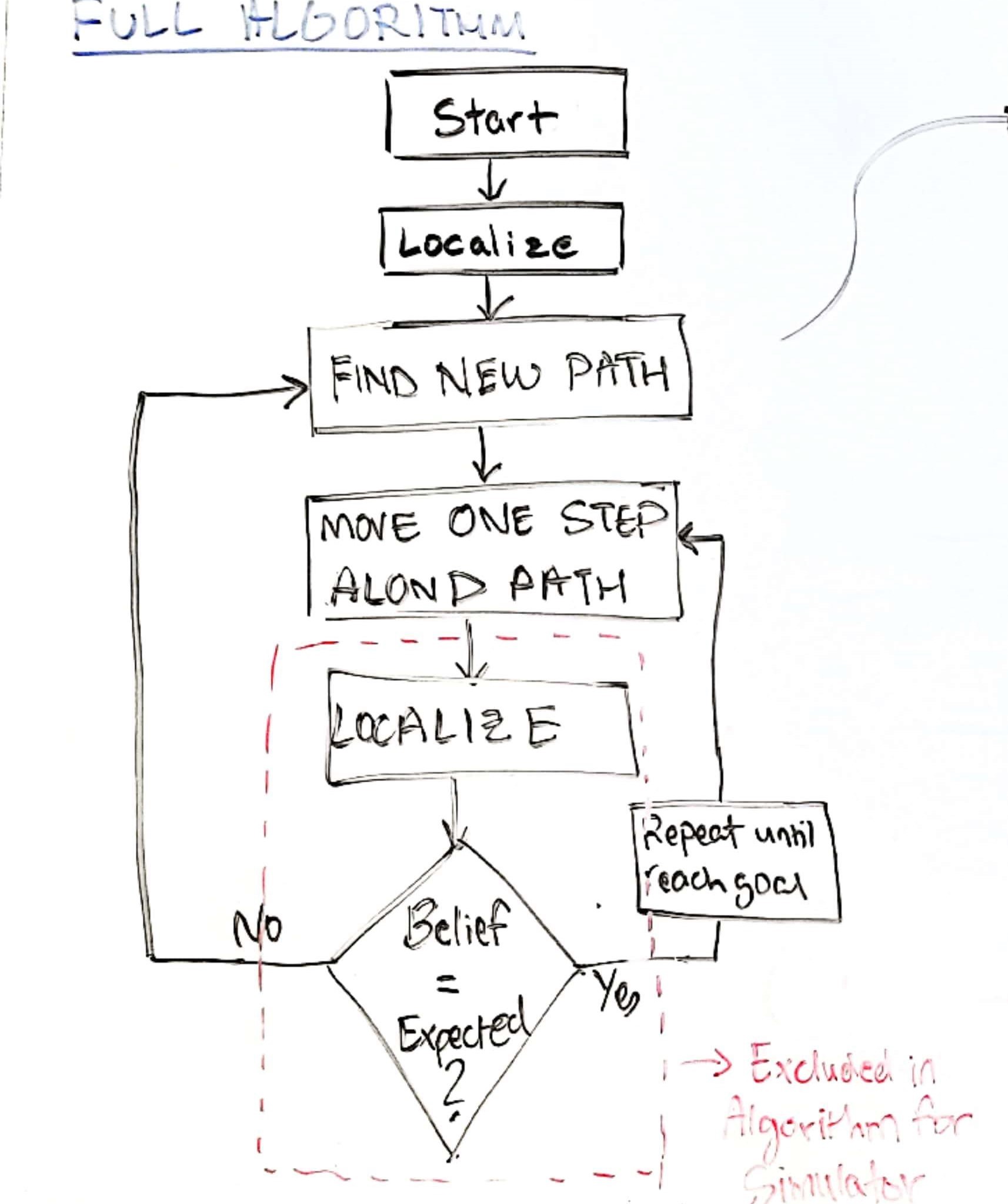
Full algorithm
Finally, putting it all together, there are three parts of the code that are important towards the process of the robot starting from an unknown location and planning a path to the goal position. Note: Not included here, but the start and goal points were determined randomly using planner_query.py, and inputed manually into the algorithm for the robot to find a path. Trajectory function
def __init__(self, loc):
self.loc = loc
self.robot = loc.robot
self.mapper = loc.mapper
# Path Planning
grid=[0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,
0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,
0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,
0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,
0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,
1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,
1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,
1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,
1,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,1,
1,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,0,0,1,
1,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,0,0,1,
1,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,1,
1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,
1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,
1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,
1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,
1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,
1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,
1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
# Convert the 1D list into a 1D numpy array
grid = np.array(grid, dtype=np.uint8)
# Convert the 1D numpy array into an appropriate 2D numpy array
grid.resize(20,20)
start = [14, 7]
goal = [2, 16]
# Get direction in which the robot needs to rotate
direction = loc.findWaypoints(grid,start,goal)
# Grid info
maxX = 1.0414
maxY = 1.1684
n = 20;
dx = maxX/(n-1);
dy = maxY/(n-1);
# Iterate through steps
s = {}; rot2_vel = 0;
time = 1; rot1_prev = 0;
for i in range(0,len(direction)):
#Given direction, go...
if (direction[i] == 0): # North
rot1_vel = (np.pi/2-rot1_prev)/time; trans_vel = dy/time;
rot1_prev = np.pi/2;
elif (direction[i] == 1): # South
rot1_vel = -(np.pi/2-rot1_prev)/time; trans_vel = dy/time;
rot1_prev = -np.pi/2;
elif (direction[i] == 2): # East
rot1_vel = (0 - rot1_prev)/time; trans_vel = dx/time;
rot1_prev = 0;
elif (direction[i] == 3): # West
rot1_vel = (np.pi-rot1_prev)/time; trans_vel = dx/time;
rot1_prev = np.pi;
input = [(rot1_vel, time), (trans_vel, time), (rot2_vel, time)]
s = {**s, **{i:input}}
self.vel_cmds = s
self.total_time_steps = len(self.vel_cmds)
# Find waypoints
def findWaypoints(self,grid,start,goal):
curr = start;
rg = goal[0]; cg = goal[1];
direction = []; min_dist = 100;
while curr != goal:
r = curr[0]
c = curr[1]
d_N = np.sqrt((rg-(r-1))**2 + (cg-c)**2)
d_S = np.sqrt((rg-(r+1))**2 + (cg-c)**2)
d_E = np.sqrt((rg-r)**2 + (cg-(c+1))**2)
d_W = np.sqrt((rg-r)**2 + (cg-(c-1))**2)
# Check which one is closest and not a wall
if grid[r-1,c]==0 and d_N < min_dist:
min_dist = d_N; new = [r-1,c]; NSEW = [0];
if grid[r+1,c]==0 and d_S < min_dist:
min_dist = d_S; new = [r+1,c]; NSEW = [1];
if grid[r,c+1]==0 and d_E < min_dist:
min_dist = d_E; new = [r,c+1]; NSEW = [2];
if grid[r,c-1]==0 and d_W < min_dist:
min_dist = d_W; new = [r,c-1]; NSEW = [3];
curr = new;
direction = np.concatenate((direction,NSEW),axis=0)
return direction
# Reset Plots
robot.reset()
loc.plotter.reset_plot()
# Init Uniform Belief
loc.init_pose()
# Get Observation Data by executing a 360 degree rotation motion
loc.get_observation_data()
# Run Update Step
loc.update_step()
loc.print_update_stats(plot_data=True)
# Get traj commands
traj = Trajectory(loc)
# Run through each motion steps
for t in range(0, traj.total_time_steps):
print("\n\n-----------------", t, "-----------------")
prev_odom, current_odom, prev_gt, current_gt = traj.execute_time_step(t)
# Prediction Step
loc.prediction_step(current_odom, prev_odom)
loc.print_prediction_stats(plot_data=True)
# Get Observation Data by executing a 360 degree rotation motion
loc.get_observation_data()
# Update Step
loc.update_step()
loc.print_update_stats(plot_data=True)
print("-------------------------------------")
Results
As shown below, I ran the simulation for two scenarios and the result of each scenario had similar behavior for the theoretical path (right) and the simulator path (left). I noticed they were not completely identical and that error is due to the slippage in the wheels and the fact the rotation and translation of the robot is not as accurate as intended. For example, instead of rotating 90 degrees, the robot may rotate 89 degrees which would result in the following path to be 1 degree off. The longer the path, the more accumulation of error, which would potentially result in slanted paths rather than straight ones. Path 1 Path 2Actual Robot
Implementation
For the real robot, the implementation was exactly the same as mentioned above for the simulator. The output of the path planning algorithm are the directions NSEW from one cell to another as the robot travels from an unknown start pose to a known goal pose. This means that the only implementation left is to convert these directions into input commands for the robot to move along the path (within arduino). I wrote the code shown below to perform this task, where a direction vector is used (consists of the direction from one cell to another along the path) where the values can be any of the following:- North = 0
- South = 1
- East = 2
- West = 3
Direction Vector = [2, 2, 0, 2, 0, 2, 0, 2, 2, 2, 2, 2, 2, 0, 0, 0, 0, 0]
Code
This allowed me to assign an angle of rotation for the robot which I compared with the computed yaw of the robot to make it accurately rotate to this desired angle. After testing, I chose a time delay that would provide the apporpriate translaton of the robot. All of this is shown in the code below, but the parts that were not included are aspects of the process acquired from previous labs i.e. localization (initial pose).
void loop(void)
{
if (STOP == 0) {
// Direction matrix
int dir[] = {2, 2, 0, 2, 0, 2, 0, 2, 2, 2 , 2, 2, 2, 0, 0, 0, 0, 0,0};
float dx = 54.8;
float dy = 61.5;
int angle2rotate;
float dist2move;
// Loop through direction vector obtained from path planning algorithm
int anglePrev = 0;
for (int i = 0; i <= 18; i++) {
Serial.println("------------------------------------------------");
Serial.print("i");
Serial.print(i);
Serial.println("");
// -------------------- Determine angle to rotate ------------------- //
if (dir[i] == 0) { // North
angle2rotate = 90 - anglePrev; anglePrev = 90;
dist2move = dy;
}
else if (dir[i] == 1) { // South
angle2rotate = 270 - anglePrev; anglePrev = 270;
dist2move = dy;
}
else if (dir[i] == 2) { // East
angle2rotate = 0 - anglePrev; anglePrev = 0;
dist2move = dx;
}
else if (dir[i] == 3) { // West
angle2rotate = 180; anglePrev = 180;
dist2move = dx;
}
Serial.print("Rotate Angle = ");
Serial.print(angle2rotate);
Serial.println("");
Serial.print("Distance translate = ");
Serial.print(dist2move);
Serial.println("" );
// ----------------Rotate until reached the desired angle ----------------- //
if (angle2rotate != 0) {
Rotate(angle2rotate);
}
// ----------------Rotate until reached the desired angle ----------------- //
Translate(dist2move);
// ------------------------ STOP Motors ------------------------ //
digitalWrite( LEDPIN, LEFT_MOTOR );
digitalWrite( LEDPIN, RIGHT_MOTOR );
myMotorDriver.setDrive( LEFT_MOTOR, 1, 0);
myMotorDriver.setDrive( RIGHT_MOTOR, 1, 0);
}
STOP = 1; // stop completely
}
else {
// ------------------------ STOP Motors ------------------------ //
digitalWrite( LEDPIN, LEFT_MOTOR );
digitalWrite( LEDPIN, RIGHT_MOTOR );
myMotorDriver.setDrive( LEFT_MOTOR, 1, 0);
myMotorDriver.setDrive( RIGHT_MOTOR, 1, 0);
}
}
// ------------------------------------------------------------------------------------------------
// function to rotate the robot a certain angles
// ------------------------------------------------------------------------------------------------
void Rotate(int angle) {
// rotate until reached desired angle
int j = 0; int offsetang = 10;
Serial.print("First YAW = ");
Serial.print(yaw);
Serial.println("");
while (abs(yaw) < (abs(angle) - offsetang)) {
Serial.println(yaw);
// ------------------------ Calculate Yaw and ang. vel------------------------ //
if (j == 0) { // skip first iteration
j++; timecurr = millis(); yaw = 0;
}
else { // everything except first iteration
{
if ( myICM.dataReady() ) {
myICM.getAGMT(); // The values are only updated when you call 'getAGMT'
// yaw from Gyro
timecurr = millis();
dt = (timecurr - timeprev) / 1000;
yaw = yaw + (myICM.gyrZ()) * dt;
thd = myICM.gyrZ();
Input = thd;
}
// --------------------------------- PID --------------------------------- //
myPID.Compute();
// ------------------------ Move Motors ------------------------ //
if (angle > 0) { // Check if angle is negative or positive
digitalWrite( LEDPIN, LEFT_MOTOR );
digitalWrite( LEDPIN, RIGHT_MOTOR );
myMotorDriver.setDrive( LEFT_MOTOR, 1, 230); //Rotate
myMotorDriver.setDrive( RIGHT_MOTOR, 1, 230);
}
else { // Check if angle is negative or positive
digitalWrite( LEDPIN, LEFT_MOTOR );
digitalWrite( LEDPIN, RIGHT_MOTOR );
myMotorDriver.setDrive( LEFT_MOTOR, 0, 230); //Rotate
myMotorDriver.setDrive( RIGHT_MOTOR, 0, 230);
}
}
}
timeprev = timecurr;
}
yaw = 0;
// ------------------------ STOP Motors ------------------------ //
digitalWrite( LEDPIN, LEFT_MOTOR );
digitalWrite( LEDPIN, RIGHT_MOTOR );
myMotorDriver.setDrive( LEFT_MOTOR, 1, 0); //Rotate
myMotorDriver.setDrive( RIGHT_MOTOR, 1, 0);
Serial.println("Done Rotating");
}
// ------------------------------------------------------------------------------------------------
// function to translate the robot a certain distance
// ------------------------------------------------------------------------------------------------
void Translate(float distwant) {
// ------------------------ Move Motors ------------------------ //
digitalWrite( LEDPIN, LEFT_MOTOR );
digitalWrite( LEDPIN, RIGHT_MOTOR );
myMotorDriver.setDrive( LEFT_MOTOR, 0, 180);
myMotorDriver.setDrive( RIGHT_MOTOR, 1, 180);
float del = distwant / 520 * 1000;
Serial.print("del = ");
Serial.print(del);
Serial.println("");
delay(del);
// ------------------------ STOP Motors ------------------------ //
digitalWrite( LEDPIN, LEFT_MOTOR );
digitalWrite( LEDPIN, RIGHT_MOTOR );
myMotorDriver.setDrive( LEFT_MOTOR, 1, 0);
myMotorDriver.setDrive( RIGHT_MOTOR, 1, 0);
delay(2000);
Serial.println("Done Translating");
}
Results
As shown below, the result of the real robot trying to plan a path from a start position to a known goal position. I used the same example as shown above, and the robot does follow the path for the most part. However, this path is not completely accurate to the theoretical or the simulated path, which may be due to the following reasons:- Even after using yaw to get the rotation to be more accurate, the robot would surpass the desired angle or rotate too little, which would mess up the entire trajectory. To solve this issue, one can localize at each waypoint and recompute the path to follow, this will add additional time for the robot but will result in more accurate outcomes.
- The translation is also inaccurate, therefore, the final pose was away from the intended final pose which can be solved by reducing the slippage of the wheels, and optimizing the delay with more testing. I initially tried to use the distance sensor as a means of checking if the translation is a certain amount or not, however, the error from the sensor affected the outcome. Later on I realized the error was coming from a different place.
- Finally, using a grid may result in errors in computation. To reduce this error, a smaller grid can be used (more number of cells) which will increase computation and process time but will result in relatively accurate outcomes.
Code for using a distance sensor to check translation
void Translate(int distwant) {
distanceSensor.startRanging(); //Write configuration bytes to initiate measurement
// ------------------------ Measure initial distance ------------------------ //
int initDist = distanceSensor.getDistance(); //Get the result of the measurement from the sensor
int ddist;
Serial.print("Wanted change in Distance = ");
Serial.print(distwant);
Serial.println("");
Serial.print("Current change in Distance = ");
Serial.print(ddist);
Serial.println("");
Serial.print("Initial Distance = ");
Serial.print(initDist);
Serial.println("");
// ------------------------ Move until reached distance ------------------------ //
while (ddist < distwant) {
// ------------------------ Move Motors ------------------------ //
digitalWrite( LEDPIN, LEFT_MOTOR );
digitalWrite( LEDPIN, RIGHT_MOTOR );
myMotorDriver.setDrive( LEFT_MOTOR, 0, 0); //Rotate
myMotorDriver.setDrive( RIGHT_MOTOR, 1, 0);
delay(10);
// ------------------------ Measure distance at each time step ------------------------ //
int currDist = distanceSensor.getDistance(); //Get the result of the measurement from the sensor
ddist = initDist - currDist;
Serial.print("Initial Distance = ");
Serial.print(initDist);
Serial.print("Current Distance = ");
Serial.print(currDist);
Serial.print("Current change in Distance = ");
Serial.print(ddist);
Serial.print("Wanted change in Distance = ");
Serial.print(distwant);
Serial.println("");
}
// ------------------------ STOP Motors ------------------------ //
digitalWrite( LEDPIN, LEFT_MOTOR );
digitalWrite( LEDPIN, RIGHT_MOTOR );
myMotorDriver.setDrive( LEFT_MOTOR, 1, 0); //Rotate
myMotorDriver.setDrive( RIGHT_MOTOR, 1, 0);
distanceSensor.clearInterrupt();
distanceSensor.stopRanging();
Serial.println("Done Translating");
}